Subsets I
Given an integer array nums, return all possible subsets (the power set).
The solution set must not contain duplicate subsets.
Example 1:
Input: nums = [1,2,3]
Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
Example 2:
Input: nums = [0]
Output: [[],[0]]중복이 없는 array의 모든 부분집합을 구하는 문제이다. 아래에 소개한 방법처럼 recursive하게 풀 수도 있겠으나, 배열에 중복이 없으므로 각 원소는 각 부분집합에 속하는가/속하지 않는가의 두 가지 가능성밖에 없고, 결론적으로 2^n 개의 부분집합이 존재하게 된다. 이는 bitmask를 이용하여 간단하게 해결할 수 있다.
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
bitmasks = [bin(i)[2:].zfill(len(nums)) for i in range(2 ** len(nums))]
answer = []
for bitmask in bitmasks:
answer.append([nums[idx] for idx, x in enumerate(bitmask) if x=='1'])
return answer배열의 길이(n)와 동일한 길이의 bitmask를 2^n개의 경우의 수 모두에 대해 생성한다. bitmask[i] == 1이면, nums[i]가 subset에 포함된다는 의미이다. 이런식으로 모든 subset을 구할 수 있다.
Subsets II
Given a collection of integers that might contain duplicates, nums, return all possible subsets (the power set).
Note: The solution set must not contain duplicate subsets.
Example:
Input: [1,2,2]
Output:
[
[2],
[1],
[1,2,2],
[2,2],
[1,2],
[]
]
위와 거의 동일하지만, 이번에는 중복이 있는 array에서 중복 없이 가능한 모든 부분집합을 구하는 문제이다. 위의 문제처럼, bitmask를 이용하면서 중복 체크를 하는 방법도 있긴 하다. 다만 이 경우, 실제 부분집합의 갯수는 2^n개보다 훨씬 적음에도 불구하고 2^n개의 경우의 수를 모두 살펴봐야 하기 때문에 비효율적이다.
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
nums.sort() # 효율적인 중복 체크를 위해, nums를 소팅하고 시작한다
bitmasks = [bin(i)[2:].zfill(len(nums)) for i in range(2 ** len(nums))]
answer = []
for bitmask in bitmasks:
tmp = [nums[idx] for idx, x in enumerate(bitmask) if x=='1']
if tmp not in answer: answer.append(tmp)
return answer
다른 방법이 있는지 생각해보았다. dfs로 풀 수 있을 것 같은데, 솔직히 머리가 잘 돌아가지 않아, Discussion의 leetcode.com/problems/subsets-ii/discuss/946001/python3-dfs-beat-90 을 참고했고 그 알고리즘을 정리해보았다. recursive call을 통해 해결한다. 이 문제에서의 핵심은 중복이 있는 배열이므로, 중복 처리를 위해 각 숫자가 나타난 횟수를 기록해야 한다. 그리고 이 횟수를 기반으로 각각의 숫자들을 subset에 더해나간다.
dfs는 새롭게 추가할 subset과 nums에 나타난 숫자 중 아직 추가되지 않은 숫자들을 parameter로 받는다.
from typing import List
from collections import Counter
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
num_count = Counter(nums)
answer = []
def dfs(subset: List[int], nums_to_add: List[int]):
answer.append(subset)
for i, num in enumerate(nums_to_add):
for cnt in range(1, num_count[num]+1):
tmp = subset + [num] * cnt
dfs(tmp, nums_to_add[i+1:])
dfs([], list(num_count.keys()))
return answer
예를 들어, [1,1,2] 라는 input이 들어왔을 때 이 알고리즘은 아래와 같이 동작한다.
| num | 1 | 2 |
| count | 2 | 1 |
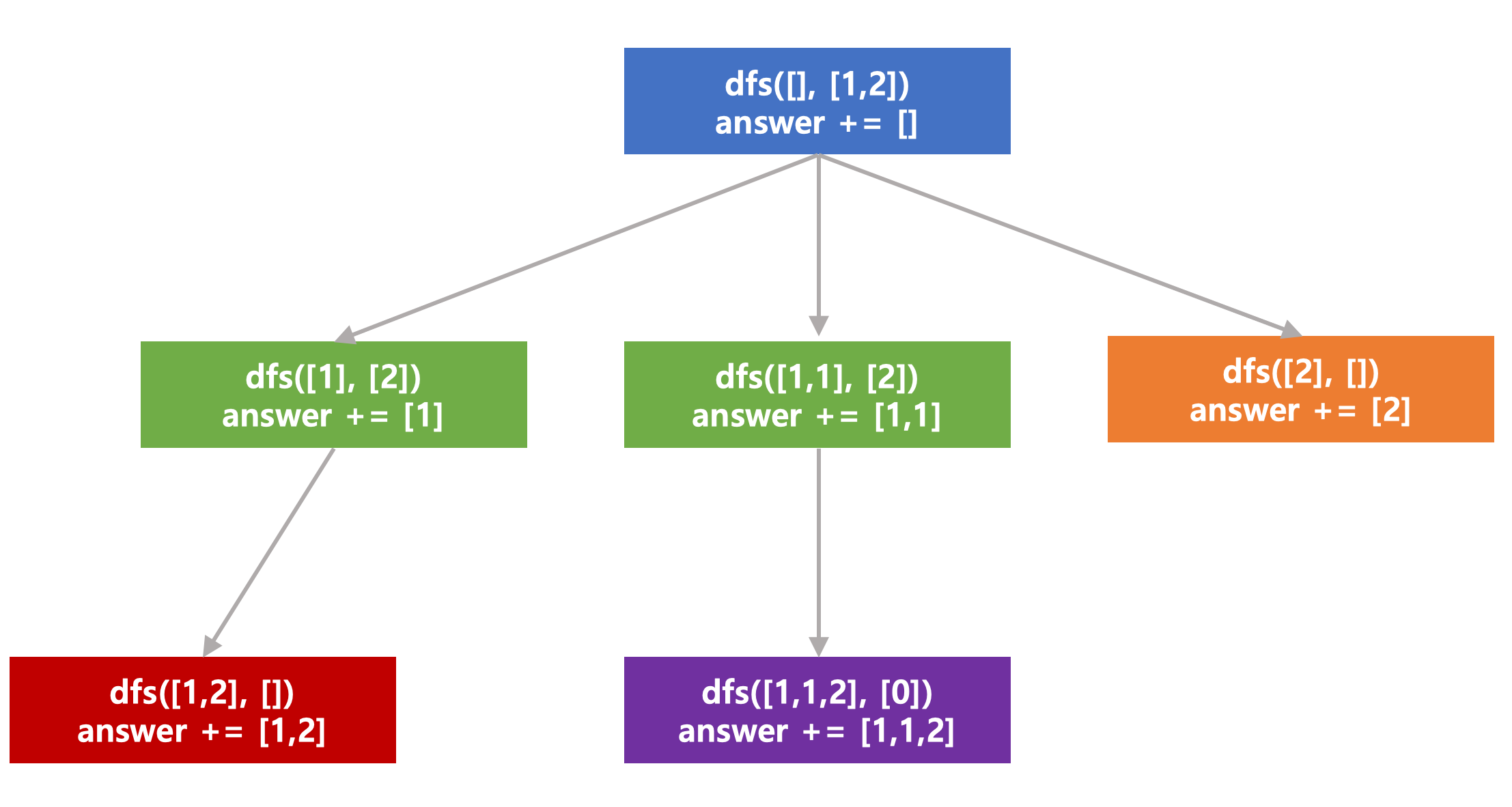
같은 색깔은, dfs 안의 같은 outer loop에서 cnt만 증가되어 돌아가는 inner loop를 의미한다.
이처럼 recursive하게 subset을 키워가며 아직 더하지 않은 숫자들을 중복 없이 subset에 추가하며 모든 subset을 구할 수 있다.
링크:
Subsets II - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
'Algorithm' 카테고리의 다른 글
| Leetcode: Longest Increasing Subsequence (LIS: 최장 증가 부분 수열) (0) | 2020.12.12 |
|---|---|
| Leetcode: Maximum Profit in Job Scheduling (0) | 2020.12.04 |
| Leetcode: Kth largest element in an Array (0) | 2020.12.03 |
| Leetcode: Linked List Random Node (Reservoir Sampling: 저수지 샘플링) (0) | 2020.12.03 |
| Leetcode: Course Schedule II (0) | 2020.12.02 |
