We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].
You're given the startTime , endTime and profit arrays, you need to output the maximum profit you can take such that there are no 2 jobs in the subset with overlapping time range.
If you choose a job that ends at time X you will be able to start another job that starts at time X.
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job.
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.
Example 2:
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job.
Profit obtained 150 = 20 + 70 + 60.
Example 3:
Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6
Constraints:
1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
1 <= startTime[i] < endTime[i] <= 10^9
1 <= profit[i] <= 10^4
Job Scheduling문제이다. naive하게 풀자면 여러가지 방법이 있겠지만, 시간초과가 난다. 실제로 내가 생각해낸 방법들은 O(n^2)이 대부분이었어서 시간초과를 해결하느라 하루종일 끙끙댔다 (T T)
# Time Limit Exceeded
class Solution:
def jobScheduling(self, startTime: List[int], endTime: List[int], profit: List[int]) -> int:
n = len(startTime)
job_schedules = sorted(zip(startTime, endTime, profit), key=lambda k: (k[0], k[1]))
sorted_end_time = [job_schedules[i][1] for i in range(n)]
dp = [job_schedules[i][2] for i in range(n)] # dp[i]: i번째 element를 넣을 때의 maximum profit값
answer = 0
for i, (start, end, pro) in enumerate(job_schedules):
prev_profits = [dp[x] for x in range(i) if sorted_end_time[x] <= start]
if prev_profits:
dp[i] += max(prev_profits)
answer = max(answer, dp[i])
return answer
dp[i]는 i번째 element를 넣었을 때의 maximum profit값으로 설정했다. (이게 불행의 시작이었다)
i번째 element를 넣었을 때의 maximum profit은, i 이전의 job중 end 가 i번째 job의 start보다 같거나 작은 것들 중 max profit을 가지는 것에 i번째 job의 profit을 더하는 식으로 구할 수 있다. 대부분의 경우 답을 구할 수 있지만, leetcode.com/submissions/detail/427083378/testcase/ 와 같은 엄청난 테스트케이스의 경우 시간초과가 났다.
결국에 Leetcode의 Discussion부분을 참고했는데, dp[i]가 의미하는 바를 조금 바꾸면, O(nlogn)에 풀 수 있다.
dp[i]가 의미하는 바는, i번째 element까지 살펴보았을 때의 maximum profit이다.
그렇다면 dp[i]의 후보가 될 수 있는 것은 두 가지이다.
(1) job[i]가 들어가는 경우: job[i]와 겹치지 않으며 i와 가장 가까운 (가장 큰 인지, 작은 인지는 dp 배열을 채워나가는 방향이 left-to-right이냐 right-to-left이냐에 따라 다름) j에 대하여 dp[j] + job[i]의 profit
(2) job[i]가 들어가지 않는 경우: 바로 직전에 구한 dp값 (i-1 혹은 i+1, dp 배열을 채워나가는 방향에 따라 다름)
따라서 점화식은 dp[i] = max((1), (2))가 된다.
dp를 왼쪽에서 오른쪽 방향(0 -> n-1)으로 채울 수도 있고, 오른쪽에서 왼쪽 방향(n-1 -> 0)으로 채울 수도 있는데, 이 솔루션에서는 후자를 택해서 풀이한다.
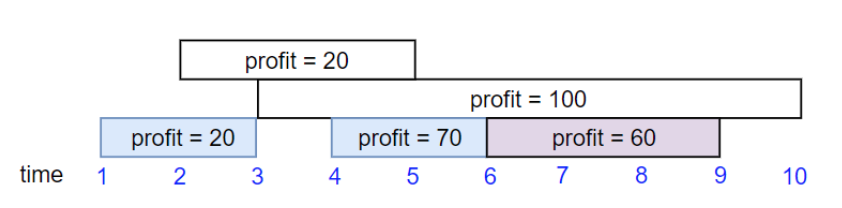
우선, 주어진 job들을 startTime순으로 소팅한다. 예를 들어 위의 예시에서는 아래와 같이 소팅된다. [startTime, endTime, profit] 순서
| Job | job[0] | job[1] | job[2] | job[3] | job[4] |
| [start,end,profit] | [1,3,20] | [2,5,20] | [3,10,100] | [4,6,70] | [6,9,60] |
이제, 위의 점화식을 구하는 부분에서의 (1)번을 계산하기 위해, 이 job들의 끝에서부터 오른쪽에서 왼쪽 순서로, 현재까지 살펴본 job들 중 각 job과 겹치지 않는 leftmost job의 위치를 구한다.
예를 들어, job[1], 즉 [2,5,20]에 대하여 구한다고 할 때, 이전까지 살펴본 [3,10,100], [4,6,70], [6,9,60]에 대하여 [startTime: 2, endTime: 5]와 겹치지 않는 job중 [2,5,20]에 가장 가까운 것은 job[4]인 [6,9,60]이다. 그렇기 때문에, 이 때의 dp값 dp[1]은
(1) dp[4] + 20 (job[1]의 profit)
(2) dp[2]
중 max값이 된다.
이 때, 다섯번째 job이 우리가 찾는 위치라는 것을 찾는 것이 관건인데, 이 때에 python의 bisect를 사용한다. 이 모듈을 이용하면 정렬된 리스트값에 특정 값 x를 insert할 때에, 어느 인덱스에 insert해야 하는지를 쉽게 알 수 있다. bisect_left는 동일한 원소가 있을 때 왼쪽의 index를, bisect_right는 오른쪽의 index를 리턴한다. 이것을 이용하면 O(logn)에 우리가 원하는 위치를 찾을 수가 있다. (자세한 내용은 Reference를 참고)
코드는 아래와 같다.
# right to left
class Solution:
def jobScheduling(self, startTime: List[int], endTime: List[int], profit: List[int]) -> int:
n = len(startTime)
job_schedules = sorted(zip(startTime, endTime, profit), key=lambda k: k[0])
start_time_sorted = [job_schedules[i][0] for i in range(n)]
dp = [0]*(n+1) # dp[i]: n-1 ~ i번째 job까지 보았을 때, maximum profit
for i in range(n-1, -1, -1):
start, end, pro = job_schedules[i]
j = bisect.bisect_left(start_time_sorted, end, i+1) # 현재까지 살펴본 job들 중, job[i]랑 겹치지 않은 leftmost element 찾기
dp[i] = max(dp[i+1], pro + dp[j]) # 이 job을 포함하지 않은 직전 profit 과 이 job을 포함하며 겹치지 않는 구간의 profit중 최대값
return dp[0]
i번째 job에 대해 살펴볼 때에, i+1번째부터의 job들에 대해서만 탐색해야 하므로 bisect의 lo값을 i+1로 세팅한다.
예를 들어, 위에서 살펴본 [1,3,20] -> [2,5,20] -> [3,10,100] -> [4,6,70] -> [6,9,60] 의 예시의 경우, job[1]인 [2,5,20]이랑 겹치지 않는 job을 찾을때에, 이 job의 endTime인 5가 들어갈 수 있는 위치를 먼저 소팅해둔 start time에서 bisect_left로 찾는다. (이것이 start time에 대하여 소팅이 필요한 이유이다) [1,2,3,4,6]에서 5가 들어갈 index는 4이므로, dp[1] = max(dp[2], 20 + dp[4])인 것을 알 수 있다. 소팅에 O(nlogn)의 시간이 소요되고, n번 도는 loop안에서 bisect를 통해 O(logn)짜리 동작이 수행되므로 최종 time complexity는 O(nlogn)이다.
위의 예시에서는 right -> left로 dp를 채워나갔는데, left -> right로 채우는 솔루션도 참고차 첨부한다. (위의 경우와 소팅기준, 비교 기준 등이 전체적으로 반대의 풀이라고 생각하면 된다.) 다만 인덱스 처리가 약간 헷갈릴 소지가 있어, 개인적으로는 위의 풀이법을 더 선호한다.
# left to right
class Solution:
def jobScheduling(self, startTime: List[int], endTime: List[int], profit: List[int]) -> int:
n = len(startTime)
job_schedules = sorted(zip(startTime, endTime, profit), key=lambda k: k[1])
end_time_sorted = [job_schedules[i][1] for i in range(n)]
dp = [0]*(n+1)
for i in range(1, n+1):
start, end, pro = job_schedules[i-1]
j = bisect.bisect_right(end_time_sorted, start, hi=i-1)
dp[i] = max(dp[i-1], pro + dp[j])
return dp[n]
링크: leetcode.com/problems/maximum-profit-in-job-scheduling/
Reference
- bisect: soooprmx.com/archives/8722
'Algorithm' 카테고리의 다른 글
| Leetcode: Minimum Operations to Reduce X to Zero (0) | 2021.01.14 |
|---|---|
| Leetcode: Longest Increasing Subsequence (LIS: 최장 증가 부분 수열) (0) | 2020.12.12 |
| Leetcode : Subsets (0) | 2020.12.04 |
| Leetcode: Kth largest element in an Array (0) | 2020.12.03 |
| Leetcode: Linked List Random Node (Reservoir Sampling: 저수지 샘플링) (0) | 2020.12.03 |
